Understanding Cosine Distance: A Key Metric in Data Science

When you venture into data science, machine learning, or even natural language processing, you’ll come across various techniques for measuring how different or similar data points are. One of the most influential and widely used methods is [cosine distance]. This article will explore what [cosine distance] is, how it works, and why it is crucial in comparing different data types. So, let’s dive in!

What Is Cosine Distance?

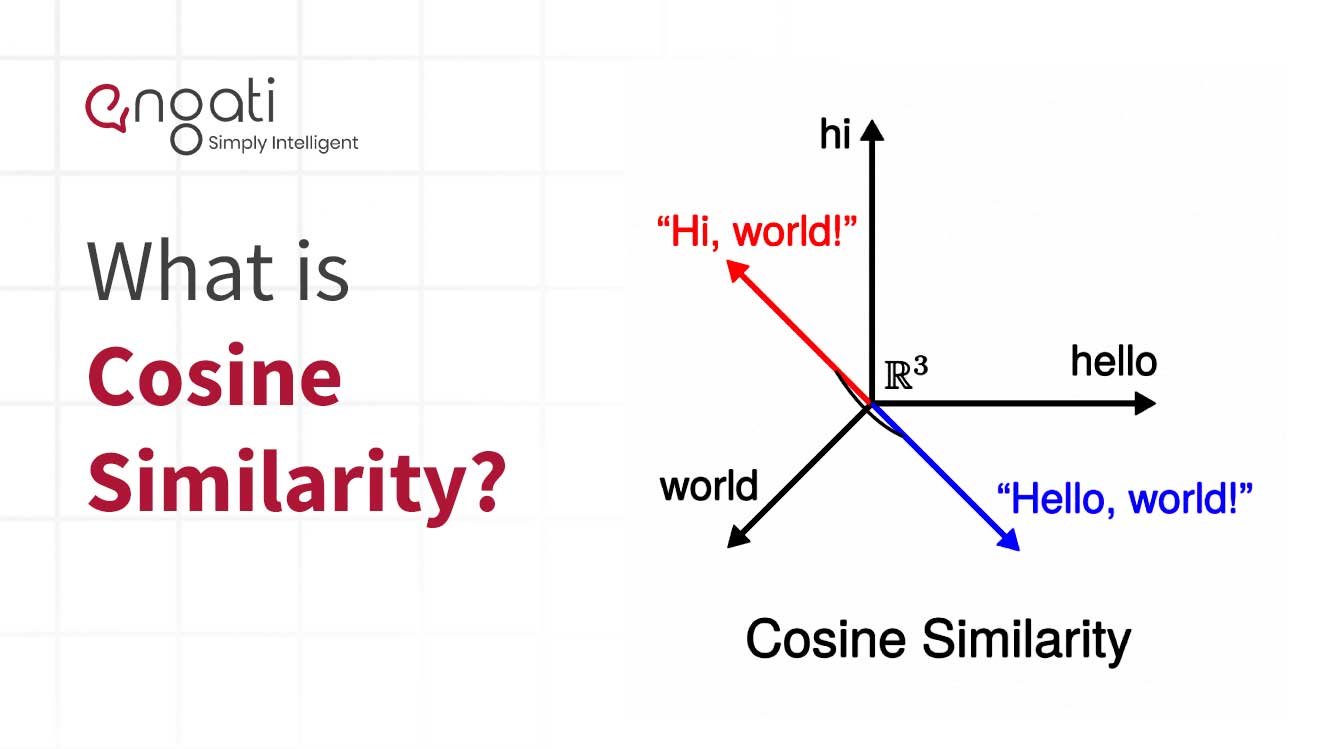
[Cosine distance] is a measure used to determine the similarity or dissimilarity between two non-zero vectors in a multi-dimensional space. It calculates the angle between these two vectors, treating them as points on a graph. Rather than focusing on the magnitude or length of the vectors, [cosine distance] only considers the direction they’re pointing in. This makes it highly effective for comparing text documents, images, and other data types where magnitude might not matter as much as the overall pattern.

In simple terms, [cosine distance] helps us determine how similar or different two data sets are based on their direction in space.

Cosine Distance vs. Cosine Similarity

You’ve probably heard of cosine similarity, which sounds much like [cosine distance], right? While they’re closely related, they serve slightly different purposes.

• Cosine similarity measures the cosine of the angle between two vectors. If the angle is slight, the vectors are similar; if the angle is large, they are dissimilar.
• [Cosine distance] is just one minus the cosine similarity. It focuses on dissimilarity rather than similarity.

So, if you have a cosine similarity of 1 (perfectly similar), the [cosine distance] will be 0. Conversely, if the cosine similarity is 0, the [cosine distance] will be 1, indicating complete dissimilarity.

The Mathematical Formula for Cosine Distance

Let’s break it down into something easier to grasp with a formula.

Cosine Similarity=A⋅B∥A∥∥B∥\text{Cosine Similarity} = \frac{A \cdot B}{\|A\| \|B\|}Cosine Similarity=∥A∥∥B∥A⋅B​

Where:

• ABA \cdot BA⋅B is the dot product of the two vectors.
• ∥A∥\|A\|∥A∥ and ∥B∥\|B\|∥B∥ are the vectors’ magnitudes (or lengths).

Once you calculate cosine similarity, you can find [cosine distance] by subtracting it from 1:

Cosine Distance=1−Cosine Similarity\text{Cosine Distance} = 1 – \text{Cosine Similarity}Cosine Distance=1−Cosine Similarity

This formula ensures that your final result is between 0 and 1, where 0 means the vectors are identical in direction, and 1 means they are entirely different.

Applications of Cosine Distance

You might wonder where and how you’d use [cosine distance] in real-world applications. It’s a vital metric in many fields, mainly when dealing with high-dimensional data.

1. Text Mining and Document Comparison

One of the most common uses of [cosine distance] is comparing text documents. Whether you’re trying to measure the similarity of two news articles or analyze the content of customer reviews, [cosine distance] comes in handy. Since text can be represented as vectors (using methods like TF-IDF or word embeddings), [cosine distance] effectively shows how close two documents are in terms of content, even if they use different words.

1. Image Recognition

Comparing two images pixel by pixel isn’t always the most efficient approach in image processing. [Cosine distance] provides a better way to compare the features of images, focusing on patterns rather than raw data. For example, facial recognition software uses [cosine distance] to compare facial features extracted as vectors, making it a powerful tool in biometric systems.

1. Recommendation Systems

Like those used by Netflix or Amazon, online recommendation systems rely on [cosine distance] to suggest new content. They compare your past behaviors (movies you’ve watched, products you’ve bought) with those of others to find similarities and predict what you might like next. This is done by converting preferences into vectors and calculating the [cosine distance] between them.

1. Natural Language Processing (NLP)

In NLP, [cosine distance] plays a massive role in word embedding techniques like Word2Vec and GloVe. These models convert words into vectors, and [cosine distance] helps determine the closeness of meanings between different words or phrases.

Why Use Cosine Distance Instead of Other Metrics?

There are numerous ways to measure similarity or distance between data points, so why choose [cosine distance]? The answer lies in its unique advantages:

• Insensitive to Magnitude: Unlike Euclidean distance, which is affected by the length of the vectors, [cosine distance] cares only about their direction. This makes it especially useful in cases where you don’t want to factor in the size of the vectors, such as text analysis or image comparison.
• Effective in High Dimensions: When working with large datasets that contain many features, [cosine distance] still performs efficiently. It easily handles high-dimensional spaces, making it ideal for modern data science tasks.
• Intuitive for Similarity Comparisons: Since it’s based on the angle between vectors, [cosine distance] provides a more intuitive similarity measure than other metrics. Two vectors that point in the same direction will have a smaller distance, regardless of their size.

Practical Example of Cosine Distance

Let’s use a simple example to illustrate how [cosine distance] works. Imagine you have two text documents, and you’ve converted them into vectors:

• Vector A: [1, 3, 0, 0, 2, 1]
• Vector B: [2, 1, 0, 1, 1, 1]

Now, using the formula for cosine similarity, you can calculate the similarity and then the [cosine distance].

Steps:

1. Calculate the dot product of A and B.
2. A⋅B=(1×2)+(3×1)+(0×0)+(0×1)+(2×1)+(1×1)=7A \cdot B = (1 \times 2) + (3 \times 1) + (0 \times 0) + (0 \times 1) + (2 \times 1) + (1 \times 1) = 7A⋅B=(1×2)+(3×1)+(0×0)+(0×1)+(2×1)+(1×1)=7
3. Calculate the magnitude of A and B.
4. ∥A∥=12+32+02+02+22+12=15\|A\| = \sqrt{1^2 + 3^2 + 0^2 + 0^2 + 2^2 + 1^2} = \sqrt{15}∥A∥=12+32+02+02+22+12​=15​ ∥B∥=22+12+02+12+12+12=8\|B\| = \sqrt{2^2 + 1^2 + 0^2 + 1^2 + 1^2 + 1^2} = \sqrt{8}∥B∥=22+12+02+12+12+12​=8​
5. Now, plug the values into the cosine similarity formula.
6. Cosine Similarity=715×8≈0.641\text{Cosine Similarity} = \frac{7}{\sqrt{15} \times \sqrt{8}} \approx 0.641Cosine Similarity=15​×8​7​≈0.641
7. Finally, subtract the cosine similarity from 1 to get [cosine distance]:
8. Cosine Distance=1−0.641=0.359\text{Cosine Distance} = 1 – 0.641 = 0.359Cosine Distance=1−0.641=0.359

So, the [cosine distance] between these two vectors is about 0.359, meaning they’re somewhat similar but not identical.

Table: Differences Between Cosine Distance and Other Distance Metrics

MetricDefinitionWhen to Use

Cosine Distance Measures the angle between two vectors, ignoring magnitude. It is Ideal for comparing the direction of vectors, especially in text or images.

Euclidean Distance Measures the straight-line distance between two points Use it when you want to factor in both direction and magnitude.

Manhattan Distance Measures the distance between two points along the axes at right angles. It is Useful in grid-based scenarios like city block distances.

Jaccard Distance Measures the dissimilarity between two sets. It is Good for comparing the similarity of binary or categorical data.

Limitations of Cosine Distance

While [cosine distance] is powerful, it does have its limitations. For one, it’s unsuitable for data containing many zeros, as the angle between vectors becomes less meaningful. Additionally, if you need to consider the vectors’ direction and magnitude, [cosine distance] may not be the best choice.

However, for tasks like text analysis, which focuses on comparing patterns or directions, [cosine distance] remains a top choice.

Conclusion: The Importance of Cosine Distance

In the grand scheme of data science, [cosine distance] is an invaluable tool for measuring similarity between data points. Whether you’re analyzing text documents, comparing images, or building recommendation systems, it helps provide a deeper understanding of how similar or different two pieces of data are. Its ability to ignore magnitude and focus solely on direction makes it incredibly effective, especially in high-dimensional spaces.

So, next time you’re faced with measuring similarity between vectors, don’t forget to consider [cosine distance]—it might be the key to unlocking better insights!

you may also like

Repository Pattern: